
| Gretchen and Joanne met at the library commons and picked
up from where they left off last time. Following the exercises in the Kindergarten Guide, they soon got
intrigued with some of the formations playing around with different combinations ... drifting into Forms of Beauty.
It was second nature to work symmetrically, after all that's how everything "falls into place". Pictured above is a rotated central hollow square made from four right-angled isosceles triangles, flanked by four complementary parallelograms. The formation created a lot of 135 degree angles, shared in common among the eight geometric forms. Both players saw how valuable manipulating the shapes over and over would be; knowing the lessons would have many applications. They sensed the relationships and enjoyed the pleasing results, at times without really understanding why. They were happy to make things opposed to having to mathematically (abstractly) "figure them out". Generally, they tried to transform what they had into what was new so that would only move what was necessary. |
Gretchen and Joanne were determined to finish the section in the
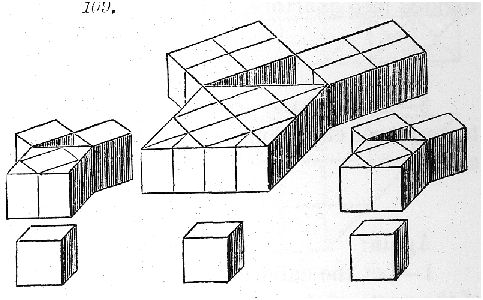
Kindergarten Guide to the end, which lays out a model of the Pythagorean Theorem. Now, Froebel's demonstration of the Pythagorean
Theorem has to be one of the simplest of all! One simply starts with four equal cubes, and combines the quarter parts of one of the cubes to another cube to make a larger cube (the "quarter squares" of one added to each side of another). The resulting length of the side of this larger cube becoming the hypotenuse of a "hollow" triangle that is formed when the other two cubes are cornered at right angles. The corners touch at this point as well at two adjacent points of the larger cube to complete making the other two sides of the right-angled triangle, which are each the length of the two equal cubes. Since the Theorem states that A2 + B2 = C2, where A and B are the length of the sides of the triangle, and C the length of its hypotunuse, knowledge of the sides is used to solve for the length of the hypotunuse. Whereby, 12 + 12 = C2 or 1 + 1 = C2, where C equals the square root of 2 or 1.4 inches. |
July 29, 2014 Next Slide Copyright © 2013-2016 savefroebel.com Research and Development Center
Joanne Hardinger and Gretchen King
A Frank Lloyd Wright Save Is A Froebel's Kindergarten Save
Wally Rogers, Founder and Director All rights reserved.